arctan计算公式
tan(arctana)=a
arctan计算公式
tan(arctan a ) = a;
arctan(-x) = -arctan x;
arctan A + arctan B= arctan(A+B)/(1-AB);
arctan x + arctan (1/x) =π/2。
反三角函数中的反正切,一般大学高等数学中有涉及。反三角函数并不能狭义的理解为三角函数的反函数,是个多值函数。它是反正弦Arcsin x,反余弦Arccos x,反正切Arctan x,反余切Arccot x这些函数的统称,各自表示其正弦、余弦、正切、余切为x的角。
两角和与差的正弦余弦正切公式
sin(α±β)=sinα·cosβ±cosα·sinβ,cos(α+β)=cosα·cosβ-sinα·sinβ,tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)。
两角和(差)公式包括两角和差的正弦公式、两角和差的余弦公式、两角和差的正切公式。两角和与差的公式是三角函数恒等变形的基础,其他三角函数公式都是在此公式基础上变形得到的。正弦公式是描述正弦定理的相关公式,而正弦定理是三角学中的一个基本定理,它指出:在任意一个平面三角形中,各边和它所对角的正弦值的比相等且等于外接圆的直径。几何意义上,正弦公式即为正弦定理。
先利用单位圆(向量)推到两角和与差的余弦公式,再利用诱导公式推导正弦公式,最后利用同角三角函数的基本关系推到正切公式。
正弦和差公式始终是sin与cos相乘; 余弦和差公式始终是cos与cos相乘,sin与sin相乘,两角和与差的正弦公式:正=正余余正符号同两角和与差的余弦公式:余=余余正正符号异。
两角和、差的正弦公式
sin(α+β)=sinαcosβ+cosαsinβ
sin(α-β)=sinαcosβ-cosαsinβ
记忆方式:异名同号
正弦的展开肯定就是以正弦开头,然后满足异名,正弦配余弦,符号就和我们要求的符号相同。
两角和、差的余弦公式
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
记忆方式:同名异号
余弦的展开肯定就是以余弦开头,然后满足同名,余弦配余弦,正弦配正弦,符号就和我们要求的符号相异。
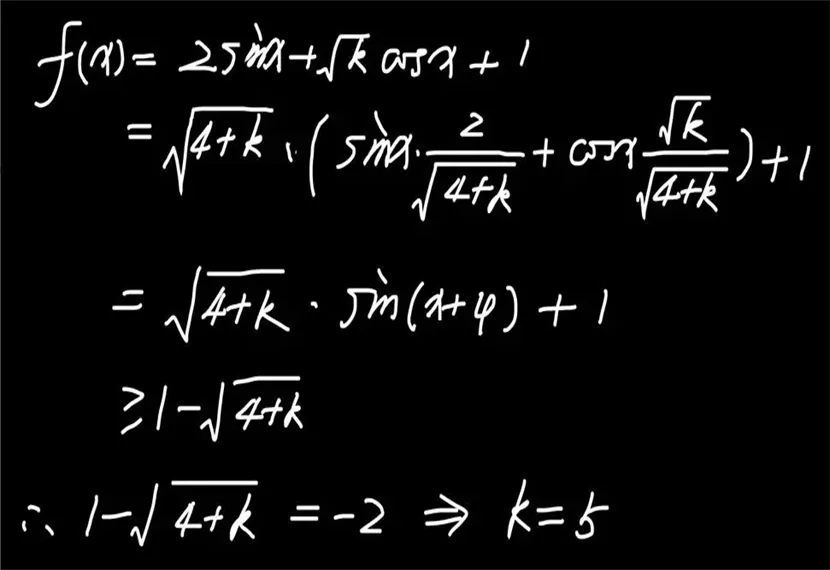
补充
倍角公式
Sin2A=2Sin*CosA
Cos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1
tan2A=(2tanA)/(1-tanA^2)
注:SinA^2 是sinA的平方 sin2(A)
两角和差
cos(α+β)=cosα·cosβ-sinα·sinβ
cos(α-β)=cosα·cosβ+sinα·sinβ
sin(α±β)=sinα·cosβ±cosα·sinβ
tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)
tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)
半角公式
tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA)
cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA
sin^2(a/2)=(1-cos(a))/2
cos^2(a/2)=(1+cos(a))/2

