有理数集是什么
由所有有理数所构成的集合,用黑体字母Q表示
数学万花筒绚丽多姿,变化万千。一个小小的数学知识只不过是整片数学之海中的一朵小浪花,就好比有理数知识只不过是数学这颗参天大树中的一个小分支。那么有理数集是什么呢?如果感兴趣的话不妨继续查看下去哦。

有理数集简介
数学上,有理数是一个整数a和一个非零整数b的比,例如3/8,通则为a/b。0也是有理数。有理数是整数和分数的集台,整数也可看做是分母为一的分数。
有理数与分数的区别,分数是—种比值的记法。可以是无理数,例如根号2/2。
有理数的小数部分是有限或为无限循环的数。不是有理数的实数称为无理数,即无理数的小数部分是无限不循环的数。
有理数集,即由所有有理数所构成的集合,用黑体字母Q表示。有理数集是实数集的子集。
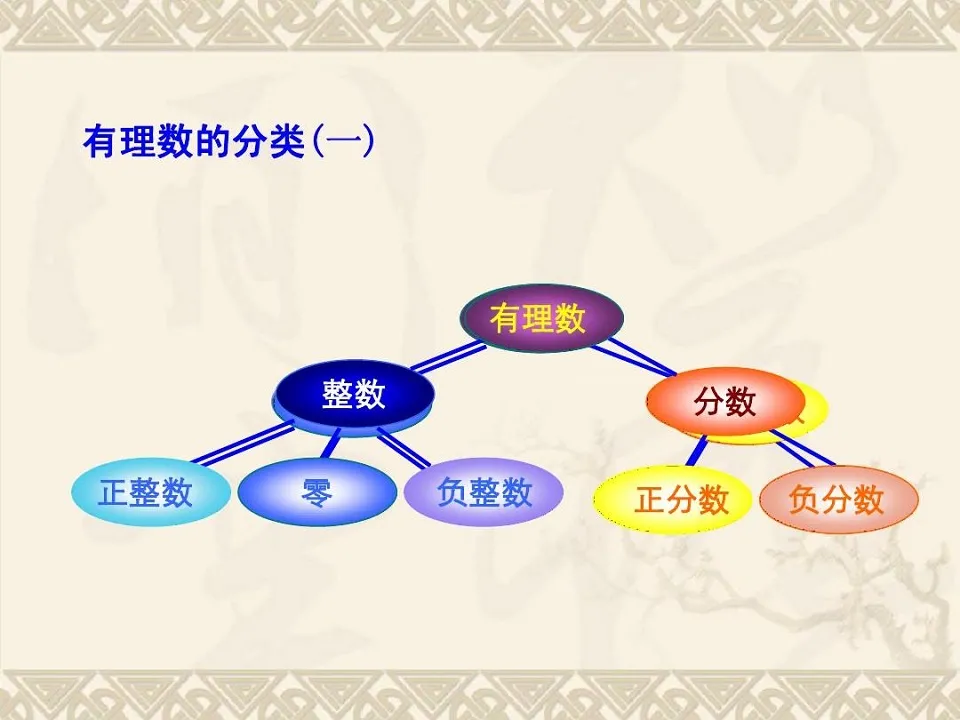
有理数指整数可以看作分母为1的分数。正整数、0、负整数、正分数、负分数都可以写成分数的形式,这样的数称为有理数(rational number)。有理数的小数部分是有限或循环小数。不是有理数的实数遂称为无理数。
有理数名字的由来
有理数这一概念最早源自西方《几何原本》,明末数学家徐光启和学者利玛窦翻译《几何原本》,前6卷时的底本是拉丁文,他们将这个词的拉丁文(即“logos”)译为“理”,这个“理”在文言文中的意思是“比值”。
明末时期日本落后于我们,常常浜使者来我国,这个有理数的睨念也被他们拿走了,但是当时的日本学者对我国的文言文理解不够,直接将在文言文中表示“比值'的“理”直译成了“道理”的“理”,没文化真坑人呀!
直到清潮中期我国对有理数的翻泽并没有错,可是到了清末,即时候中国落后于日本,于是清朝派留学生去日本,居然又将此名词重新传回中国,并且一直沿用至今。以致于现在中日两国都用“有理数”和"无理数”这一错误的说法。所以说现在对“有理数”名称的理解的疑惑是历史原因造成的。
有理数大小的比较
由正有理数的大小排列我们可以知道“在数轴上表示的两个数,右边的数总比左边的数大”,于是规定“数轴上右边的点所表示的数大于左边的点所表示的数。"
根据这个规定,可以知道:正数都大于0;负数都小于0;正数大于一切负数。
对于两个正数的大小,小学时我们已经知道。关于两个负数的比较大小,我们虽然已经可以根据它们在数轴上的位置确定,但是我们希望把它i
转化为正数来进行比较,这样会使计算简便。如| – 3/=3,l-
2|=2,因为3>2,所以-3>|- 2|而由数轴可知- 3<-2,即“两个负数,绝对值大的反而小”。

