外接球表面积公式?
π(a^2+b^2+c^2)
外接球表面积公式
π(a^2+b^2+c^2)
计算过程如下
设长方体的长宽高分别为a、b、c。
则外接球的直径即为长方体的体对角线
半径为:根号(a^2+b^2+c^2)/2
由球的表面积的公式为4πR^2
故表面积为:π(a^2+b^2+c^2)
补充
设一个长方体的长、宽、高分别为a、b、c,则它的表面积为S = (ab+bc+ca)×2,也等于2ab+2bc+2ca,还等于2(ab+bc+ca)。
公式:长方体的表面积=长×宽×2+宽×高×2+长×高×2,或:长方体的表面积=(长×宽+宽×高+长×高)×2。
三棱柱外接球表面积公式是什么
公式:S=4/3*πR2
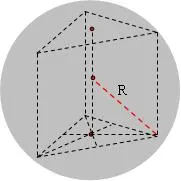
设图中正三棱柱的底面边长为a,高为h,球半径R。则底面三角形的高为(√3)a/2,于是有:
R2=(h/2)2+[(2/3)(√3)a/2)]2,因此外接球的表面积可以求出为4/3*πR2。
扩展
正三棱柱的外接球半径的求法
1、直三棱柱 正六棱柱外接的半径:关键是找到各顶点外接球的球心。
2、找到了球心,直接连接球心和任一顶点就是半径。
3、该球心的就是它们的中心; 也是正六棱柱、正三棱柱的重心,但不是直三棱柱的重心。
4、位置在两个底面外接圆的圆心(中心)的连线的中点。
5、所以要先求出两个底面的外接圆的圆心,就很容易找到这两个圆心的连线的中点。
底面三角形是正三角形,设棱长为a,底面三角形高为:√3/2a,球心在底面射影是底面三角形的外心(重心),设为M点。
AO=2a/3*√3/2=√3a/3,球心为O点,顶点为P点,PM=√a^2-(√3a/3)^2=√6a/3,从O点作ON⊥PA,△PON∽△PAM,a^2/=PO*PM。得外接球半径R=PO=√6a/4。

