圆形有几条对称轴
无数条
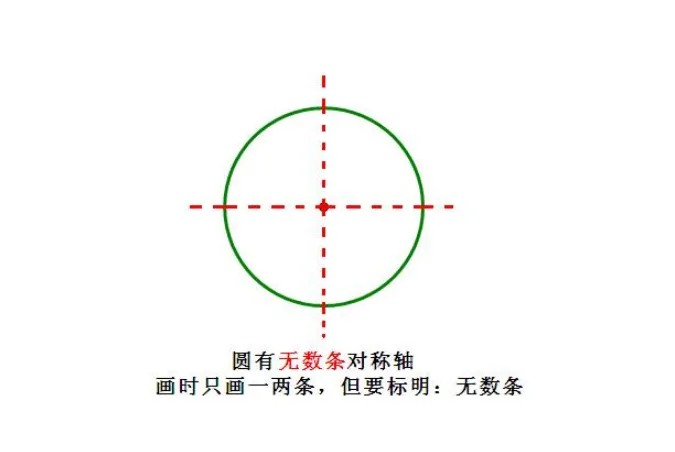
圆的对称轴就是圆的直径所在的直线,因为圆的直径有无数条。圆直径所在的直线有无数条,代表圆的对称轴有无数条。
在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周所形成的封闭曲线叫做圆。圆有无数个点。在同一平面内,到定点的距离等于定长的点的集合叫做圆。在一个平面内,一动点以一定点为中心,以一定长度为距离旋转一周所形成的封闭曲线叫做圆。圆有无数个点。
圆形是一种圆锥曲线,由平行于圆锥底面的平面截圆锥得到。圆是一种几何图形。根据定义,通常用圆规来画圆。同圆内圆的直径、半径长度永远相同,圆有无数条半径和无数条直径。圆是轴对称、中心对称图形。对称轴是直径所在的直线。同时,圆又是“正无限多边形”,而“无限”只是一个概念。当多边形的边数越多时,其形状、周长、面积就都越接近于圆。所以,世界上没有真正的圆,圆实际上只是概念性的图形。
圆形
圆是一种几何图形。当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的轨迹叫做圆。根据定义,通常用圆规来画圆。同圆内圆的半径长度永远相同,圆有无数条半径和无数条直径。圆是轴对称、中心对称图形。
对称轴是直径所在的直线。同时,圆又是“正无限多边形”,而“无限”只是一个概念。当多边形的边数越多时,其形状、周长、面积就都越接近于圆(这也是为什么人们所谓的圆只是正多边形)。所以,世界上没有真正的圆,圆实际上只是概念性的图形。圆是由古希腊数学家毕达哥拉斯发现的。
根据上述知识,可知,圆形有无数条直径,圆形的对称轴是直径所在的直线,所以圆形有无数条对称轴。
几种常见的轴对称图形和中心对称图形
轴对称图形:线段、角、等腰三角形、等边三角形、菱形、矩形、正方形、等腰梯形、圆、双曲线(有两条对称轴)、椭圆(有两条对称轴)、抛物线(有一条对称轴)等。
对称轴的条数:角有一条对称轴,即该角的角平分线;等腰三角形有一条对称轴,是底边的垂直平分线;等边三角形有三条对称轴,分别是三边上的垂直平分线;菱形有两条对称轴,分别是两条对角线所在的直线,矩形有两条对称轴分别是两组对边中点的直线;
中心对称图形:线段 、平行四边形、菱形、矩形、正方形、圆等。
对称中心:线段的对称中心是线段的中点;平行四边形、菱形、矩形、正方形的对称中心是对角线的交点;圆的对称中心是圆心。
说明:线段、菱形、矩形、正方形以及圆它们即是轴对称图形又是中心对称图形。
坐标系中的轴对称变换与中心对称变换:
点P(x,y)关于x轴对称的点P₁的坐标为(x,-y),关于y轴对称的点P₂的坐标为(-x,y)。关于原点对称的点的坐标P3的坐标是(-x,-y)这个规律也可以记为:关于y轴(x轴)对称的点的纵坐标(横坐标)相同,横坐标(纵坐标)互为相反数。 关于原点成中心对称的点的,横坐标为原横坐标的相反数,纵坐标为原纵坐标的相反数,即横坐标、纵坐标同乘以-1。

