向量积的几何意义是什么呢

向量积介绍

向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。其应用也十分广泛，通常应用于物理学光学和计算机图形学中。

向量积可以被定义为

模长：（在这里θ表示两向量之间的夹角（共起点的前提下）（0°≤θ≤180°），它位于这两个矢量所定义的平面上。）

方向：a向量与b向量的向量积的方向与这两个向量所在平面垂直，且遵守右手定则。（一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的：若坐标系是满足右手定则的，当右手的四指从a以不超过180度的转角转向b时，竖起的大拇指指向是c的方向。）

也可以这样定义（等效）：

向量积|c|=|a×b|=|a||b|sin

即c的长度在数值上等于以a，b，夹角为θ组成的平行四边形的面积。

而c的方向垂直于a与b所决定的平面，c的指向按右手定则从a转向b来确定。

运算结果c是一个伪向量。这是因为在不同的坐标系中c可能不同。

补充

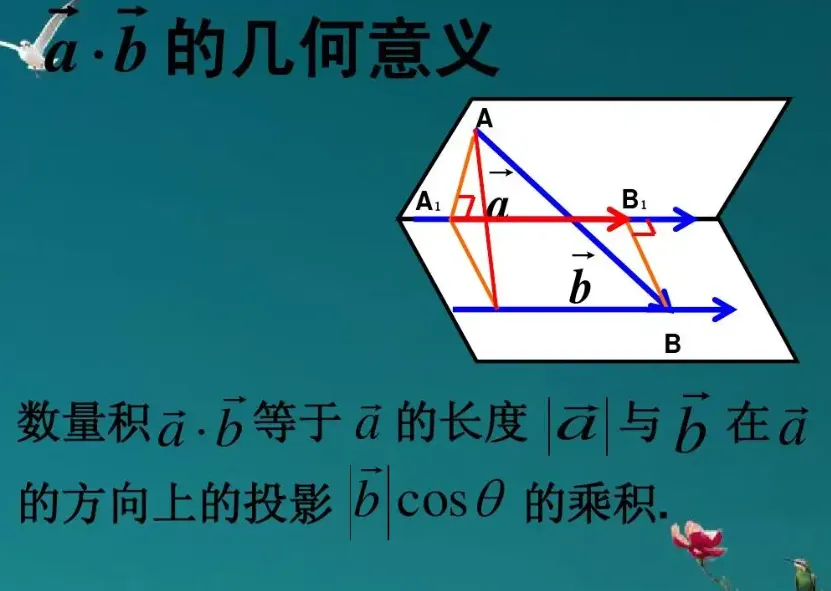
两向量的数量积等于其中一个向量的模与另一个向量在这个向量的方向上的投影的乘积

两向量α与β的数量积α·β=|α|*|β|cosθ其中|α||β|是两向量的模θ是两向量之间的夹角(0≤θ≤π)

若有坐标α(x1,y1,z1) β(x2,y2,z2)那么 α·β=x1x2+y1y2+z1z2 |α|=sqrt(x1^2+y1^2+z1^2)|β|=sqrt(x2^2+y2^2+z2^2)

把|b|cosθ叫做向量b在向量a的方向上的投影

因此用数量积可以求出两向量的夹角的余弦cosθ=α·β/|α|*|β|

已知两个向量A和B,它们的夹角为C,则A的模乘以B的模再乘以C的余弦称为A与B的数量积(又称内积、点积。)

即已知两个非零向量a和b,它们的夹角为θ,则数量|a||b|cosθ叫做a与b的数量积,记作a·b"·不可省略若用×则成了向量积。